5.4 APLICACIÓN DE LAS TRANSFORMACIONES LINEALES: REFLEXIÓN, DILATACIÓN, CONTRACCIÓN Y ROTACIÓN

Antes de comenzar hay que dejar en claro lo que es una transformación lineal y es que está es una función. Además, por ser función tiene dominio y co-dominio, con la particularidad de que éstos son unos espacios vectoriales.
Ahora bien, para finalizar con este tema de transformaciones lineales, cerramos con su aplicación el cual tiene que ver con cuatro puntos que se presentarán a continuación:
 
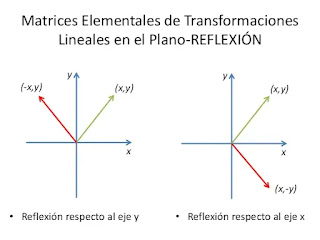
REFLEXIÓN
 
Cuando un conjunto de puntos dados es graficado desde el espacio euclidiano de entrada a otro de manera tal que este es isométrico al espacio euclidiano de entrada, la llamamos reflexión del conjunto de puntos dados. También se realiza con respecto a la matriz, en tal situación la matriz de salida es llamada la matriz de reflexión. La reflexión es realizada siempre con respecto a uno de los ejes, sea el eje x o el eje y. Esto es como producir la imagen espejo de la matriz actual.

EJEMPLO:

Sea V= (2,5) aplique la reflexión con respecto al eje Y

FÓRMULA

Sustituyendo

DILATACIÓN
 
Al igual que en la reflexión, se pueden expandir los puntos dados en una dirección particular. La expansión se realiza habitualmente para un cierto grado. Es como realizar una operación de multiplicación de los elementos del conjunto de puntos dados con un término escalar hacia la dirección donde tiene que ser expandido. Sea para un punto (2, 3) si el grado de expansión 2 es la dirección de y, entonces el nuevo punto obtenido es (2, 6).
 

EJEMPLO:

Sea V= (3,10) aplique la dilatación igual a c=6 en el eje x

FÓRMULA

Sustituyendo

CONTRACCIÓN
 
La contracción es el procedimiento inverso de la expansión. Aquí el punto es contraído en un determinado grado hacia una dirección dada. Sea el punto de entrada (4, 8) y este debe ser contraído para el grado dos en la dirección de x entonces el nuevo punto resulta ser (2, 8).

EJEMPLO:

Sea V= (18,10) aplique la contracción igual a k=2 tanto en x como en y.

FÓRMULA

Sustituyendo

ROTACIÓN
 
El término rotación tiene dos significados, pues la rotación de un objeto puede ser realizada con respecto al eje dado o al eje mismo. La rotación se realiza para un cierto grado el cual es expresado en forma de un ángulo. Asimismo, la rotación puede realizarse en la dirección de las manecillas del reloj, o inverso a las manecillas del reloj.

EJEMPLO:

Sea V= (2,4) aplique la rotación para un

FÓRMULA

Sustituyendo

 
 
VIDEOS DE APOYO